How to Master GMAT Problem Solving

The GMAT™ exam feels like a math test, especially GMAT Problem Solving problems. They read just like textbook math problems we were given in school; the only obvious difference is that the GMAT Quant section gives us five possible answer choices.

It’s true that you have to know certain math rules and formulas and concepts, but actually, the GMAT is really not a math test. First of all, the test doesn’t care whether you can calculate the answer exactly (e.g., 42). It cares only that you pick the right answer letter (e.g., B)—and that’s not at all the same thing as saying that you have to calculate the answer exactly, as you did in school.

More than that, the GMAT test-writers are looking for you to display quantitative and critical reasoning skills (the section is literally called Quantitative Reasoning); in other words, they really want to see whether you can think logically about quant topics. They’re not interested in testing whether you can do heavy-duty math on paper without a calculator. And here’s the best part: They build the problems accordingly and you can use that fact to make GMAT Problem Solving problems a whole lot more straightforward to solve. I’ll show you how in this article!

GMAC’s team (aka, the people who make the GMAT) gave me three random problems to work through with you. I had no say in the problems; I didn’t get to choose what I liked. Nope, these three are it, and every single one illustrates this principle: The GMAT is really a test of your quantitative reasoning skills, not your ability to be a textbook math whiz.

GMAT Quant is not a math test

Okay, let’s prove that claim I just made. Grab your phone and set the timer for 6 minutes. (If you’ve been granted 1.5x time on the GMAT, set it for 9 minutes. If you’ve been granted 2x time on the GMAT, set it for 12 minutes.)

Do the below 3 problems under real GMAT conditions:

• Do them in order. Don’t go back.
• Pick an answer before you move to the next one. (Don’t just say you’re not sure and move on. Make the guess, as you have to do on the real test.)
• Have an answer for all the problems by the time your timer dings—even if your answers are random guesses.

Ready? Go!

Problem #1: Fellows in the org

According to the table above, the number of fellows was approximately what percent of the total membership of Organization X? 

(A) 9%
(B) 12%
(C) 18%
(D) 25%
(E) 35%

Problem #2: Yolanda and Bob

One hour after Yolanda started walking from X to Y, a distance of 45 miles, Bob started walking along the same road from Y to X. If Yolanda’s walking rate was 3 miles per hour and Bob’s was 4 miles per hour, how many miles had Bob walked when they met?

(A) 24
(B) 23
(C) 22
(D) 21
(E) 19.5

Problem #3: Oil cans

Two oil cans, X and Y, are right circular cylinders, and the height and the radius of Y are each twice those of X. If the oil in can X, which is filled to capacity, sells for $2, then at the same rate, how much does the oil in can Y sell for if Y is filled to only half its capacity? 

(A) $1
(B) $2
(C) $3
(D) $4
(E) $8

Time’s up! Do you have an answer for each problem? If not, make a random guess—but do choose an answer for every problem.

You probably want me to tell you the three correct answers so you’ll know whether you got them right. But I’m not going to.

We’re going to review these in the same way that I want you to review them when you’re studying on your own—and that means *not* looking up the correct answer right away. 

• How confident are you about this problem?
• Did/do you have another idea for how to solve? Try it now.
• Were you straining to remember some rule or formula? Look it up and try again.
• Still stuck? Okay, look at the correct answer. Does knowing that give you any ideas? Push them as far as you can. 
• Stuck again? Start to read the explanation. Stop as soon as the explanation gives you a new idea. Push it as far as you can before you come back to the explanation again.

Basically, push your own thinking and learning as far as you can on your own. Use the correct answer and explanation only as a series of hints to help unstick yourself when you get stuck.

Okay, let’s dive in!

GMAT Problem Solving #1: Estimate

According to the table above, the number of fellows was approximately what percent of the total membership of Organization X? 

(A) 9%
(B) 12%
(C) 18%
(D) 25%
(E) 35%

We’re going to use the UPS solving process: Understand, Plan, Solve. (A mathematician named George Polya came up with this.) Use this rubric to approach any quant-based problem you ever have to figure out in your life!

The basic idea is this: Don’t just jump to solve. (That’s panic-solving! We’ve all been there. It does not end well.) Understand the info first. Come up with a plan based on what you see. Only then, solve. 

And if you don’t understand or can’t come up with a good plan? On the GMAT, bail! Pick your favorite letter and move on. UPS can help you know what to do and what not to do.

Understand

Glance at the answers. Yes, before you even read the problem! 

The answers indicate that this is a percent problem and they’re also pretty decently spread apart. One is a little less than 10% and another is a little greater than 10%, so that’s one nice split. The remaining three are a little less than 20%, exactly 25%, and about 33%, otherwise known as one-third. Those are all “benchmark,” or common, percentages, so now I know I can probably estimate to get to my answer. Excellent.

And then the problem actually includes the word approximately! Definitely going to estimate on this one.

Start building a habit of glancing at the answers on every single Problem Solving problem during the Understand phase, before you even think about starting to solve. (And yes, I really do glance at the answers before I even read the question stem!)

Here are some examples of the types of answer-choice characteristics that indicate there’s a good chance you’ll be able to estimate at least a little:

• The answers are really spread out (e.g., 10, 100, 300, 600, 900)
• Some are positive and some are negative
• Some are less than 1 and some are greater than 1
• They’re spread out on a percent scale (0 to 100) or on a probability scale (0 to 1)—less than half, greater than half, etc.

Next, there’s a table with a bunch of categories and each category is associated with a specific number. What does the question ask?

It wants to know the Fellows as a percent of the total. That’s a fraction with fellows on the top and the total of all members on the bottom:

The Fellows category is already listed in the table. Great, that’s the numerator.

What about the total? That means adding up all the numbers in the table without a calculator or Excel. Rolling my eyes. And that’s how I know that I will not be doing “textbook math” here. Pay attention to those feelings of annoyance! There’s some other easier, faster path to take. Use your Plan phase to find it.

Plan

I need the Total. I can estimate. Look at the collection of numbers. Can you group any into pairs that will add up to “nicer” numbers—numbers that end in zeros?

Here’s one way: 

• Honorary is a tiny number compared to the rest. Ignore it. 
• Fellows are a little under 10,000 and Members are a bit over 35,000. Group them. 
• Associates are a little less than 28,000 or a little more than 2,000 away from 30,000. And Affiliates are a little over 2,000! Combine those two groups.

Solve 

We’re already spilling into the solve stage on this one. Fellows and Members together are about 45,000. Associates and Affiliates together are about 30,000. Altogether, there are 75,000 members:

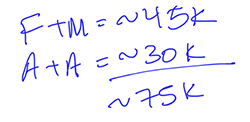
That goes on the bottom of the fraction. Fellows go on top. They’re about 9,200, so let’s call that 9,000. Make a note on your scratch paper that you’re underestimating—just in case you need to use that to choose your final answer. I use a down-arrow to remind myself.

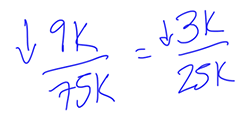
How to simplify 9 out of 75? Both of those numbers are divisible by 3.

Ok, 3 out of 25: what percent is that? We normally see percentages as “out of 100.” Hmm. 

If you multiply the denominator by 4, that gets you to “out of 100.” And whatever you do to the denominator, you have to do to the numerator, so the fraction turns into 12 out of 100, or 12%.

12% is in the answers; the next closest greater value (since we slightly underestimated) is 18%. That’s too far away, so the only answer that makes sense is (B).

Notice how the numbers looked really ugly to start out, but as soon as you started estimating, they combined and simplified really nicely? It’s not just luck. The test-writers know you don’t have access to a calculator, so they’re building the problems to work out nicely if you use these types of approaches. They actually want to reward you for using the kind of quantitative reasoning that you’d want to use at work and in business school.

You can certainly solve GMAT Problem Solving problems using traditional textbook math approaches. You’ll just do a lot more work that way. And using textbook approaches won’t actually help train your brain for the kind of analytical thinking about quant that you’ll need to do in business school or in the working world.

Free GMAT™ Prep from the Makers of the Exam

The best way to jumpstart your prep is to familiarize yourself with the testing platform and take practice tests with real GMAT exam questions.

Learn More

GMAT Problem Solving #2: Logic (and draw!) it out

One hour after Yolanda started walking from X to Y, a distance of 45 miles, Bob started walking along the same road from Y to X. If Yolanda’s walking rate was 3 miles per hour and Bob’s was 4 miles per hour, how many miles had Bob walked when they met? 

(A) 24
(B) 23
(C) 22
(D) 21
(E) 19.5

Understand

The answers are real values and on the smaller side. They’re pretty clustered, so probably won’t be estimating on this one. Four of the five are integers. I wonder whether I can work backwards on this one (i.e., just try some of the answers)?

This problem is what I call a Wall of Text—a story problem. Get ready to sketch this out. Take your time understanding the setup; if you don’t “get” the story, you’ll never find the right answer. (And if you don’t get the story, that’s your clue to guess and move on.)

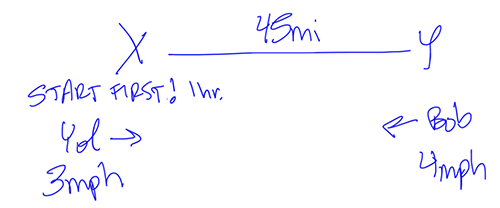
There are two people, 45 miles apart, and they’re walking towards each other. Normally, I’d only write initials for the two people, but annoyingly, Yolanda shares her initial with one of the locations.

The first sentence has a critical piece of info that’s easy to gloss over: Yolanda starts first, an hour before Bob. 

It’s super annoying that they don’t start at the same time. I don’t know what to do about that yet, but I’m noting it because I want to think about that when I get to my Plan stage. Again, pay attention to whatever annoys you about the problem! That’s why I put START FIRST in all-caps on my scratch paper.

Next, Yolanda walks a little slower than Bob. Add that to your diagram.

Finally, the problem asks who walked further by the time they meet—and how far that person walked. If Yolanda and Bob had started at the same time, then I’d know Bob walked farther, since he’s walking faster, but Yolanda started first, so I can’t tell at a glance. Still annoyed by that detail.

Plan

The two people have to cover 45 miles collectively in order to meet somewhere in the middle. Glance at the answers again. There are two sets of pairs that add to 45: (A) 24 and (D) 21 and (B) 23) and (C) 22. 

On a problem like this one, the most common trap answer is going to be solving for the wrong person (in this case, Yolanda instead of Bob). So the correct answer is going to fall into one of those pairs, because then the most common trap answer will also be built into the problem. The other pair will represent some common error when solving for Bob—and then also mistakenly solving for Yolanda instead. But answer (E) 19.5 doesn’t have a pairing, so it has no built-in trap. If you have to guess, don’t guess the unpaired answer, (E).

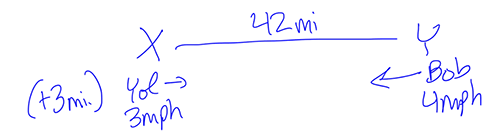
Once I subtract the 3 miles that Yolanda walked alone, the two of them together have 42 more miles to cover before they meet. I did note the extra 3 miles she walked off to the side just in case.

Bingo. Now I know how I’m going to solve this problem, because now it’s a more straightforward rate problem.

Solve

From here, you can do the classic “write some equations and solve” approach to rates problems. But I’m going to challenge you to keep going with this Logic It Out approach we’re already using—both because it really is easier and because it’s what you would use in the real world. You’re not getting ready to take the GMAT because you want to become a math professor. You’re doing this to be able to think about quant topics in a business context. So make your GMAT studies do double-duty and get you ready for b-school (and work!) as well.

Back to Bob and Yolanda. They’re 42 miles apart and walking towards each other. Every hour, Yolanda’s going to cover 3 miles and Bob’s going to cover 4 miles, so they’re going to get 7 miles closer together. Together, they’re walking 7 miles per hour.

When two people (or cars or trains) are moving directly towards each other, you can add their rates and that will tell you the combined rate at which they’re getting closer together. (You can do the same thing if the two people are moving directly away from each other—in this case, the combined rate is how fast they’re getting farther apart.)

One more thing to note: The distance still to cover is great enough (42 miles) compared to their combined rate (just 7 mph) that Bob is going to “overcome” the 3 miles that Yolanda walked on her own first. So Bob covered a greater distance than Yolanda did. The answer is going to be one of the two greater numbers in the pairs: (A) 24 or (B) 23.

So Yolanda and Bob are getting closer together at a rate of 7 miles each hour and they have a total of 42 miles to cover until they meet. How long is it going to take them?

Divide 42 by 7. They’re going to meet each other after 6 hours on the trail. At this point, Bob has spent a total of 6 hours walking, but not Yolanda! She started first, so she spent a total of 6 + 1 = 7 hours walking. The question asks how far Bob walked: 4 miles per hour for 6 hours, or a total of (4)(6) = 24 miles. 

The correct answer is (A).

If you’d solved for Yolanda first, you’d have gotten (3 miles per hour)(7 hours) = 21 miles. That’s in the answer choices, but it’s less than half of the total distance, so she wasn’t the one who walked farther. In other words, answer (D) is a trap.

Even if you do know how to solve the problem, it’s important to have done that earlier thinking to realize that the answer must be (A) or (B). That way, when you solve for Yolanda, you won’t accidentally fall for answer (D), since Yolanda’s distance is in the answer choices.

When the problem talks about two people or two angles in a triangle or two whatevers and the problem also tells you what they add up to, the non-asked-for person/angle is almost always going to show up in the answer choices as a trap. You do the math correctly, but you accidentally solve for x when they asked you for y. We’ve all made that mistake. 

Noticing that detail earlier in your process is a great way to avoid accidentally falling for the trap answer during your Solve phase.

(Have Polya and I sold you yet on using the UPS process? I hope so.)

Should I Retake the GMAT?

Should you retake the GMAT, and does retaking the GMAT look bad? Manhattan Prep’s Stacey Koprince answers the most common retake the GMAT questions.

Learn More

GMAT Problem Solving #3: Draw it out; Do arithmetic, not algebra; Choose smart numbers

Two oil cans, X and Y, are right circular cylinders, and the height and the radius of Y are each twice those of X. If the oil in can X, which is filled to capacity, sells for $2, then at the same rate, how much does the oil in can Y sell for if Y is filled to only half its capacity? 

(A) $1
(B) $2
(C) $3
(D) $4
(E) $8

Understand

Glance at the answers. Small integers. Kind of close together, so estimation might not be in the cards, but perhaps working backwards (try the answer choices) could work, depending on how the problem itself is set up. (I don’t know yet because I haven’t actually read the problem.)

Now I’m part-way into the first sentence and see the word cylinders. Overall, I’m not a fan of geometry and I really dislike 3D geometry in particular. So as soon as I see that word, part of my brain is thinking, “If this is a hard one, I’m out.”

But I’m going to finish reading it before I decide. Let’s see. Two cylinders, and then they give me some relative info about the height and radius. They’re probably going to ask me something about volume, since the volume formula uses those measures, and scanning ahead: yep, volume.

So now I know I need to jot down the volume formula and I’m also going to draw two cylinders and label them.

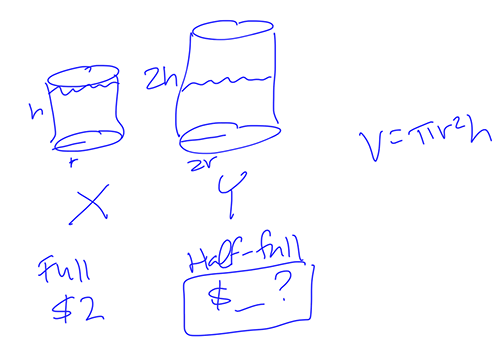
I’m going to make sure I note really clearly what I’m trying to solve for. On geometry problems in particular, it’s really easy to solve for something other than the thing they asked you for. And on this one, I’m also making an extra note that the larger cylinder is only half full. I both wrote that down and drew little water lines in the cylinders to cement that fact in my brain.

This is a complex problem, so just pause for a second here. Do you understand everything they told you, including what they asked you to find? If not, this is an excellent time to pick your favorite letter and move on.

Plan

If you are going to continue, don’t jump straight to solving. Plan first. (And if you can’t come up with a good plan, that’s another reason to get out.)

The thing that’s annoying me: They keep talking about the dimensions for the two cylinders but they never provide real numbers for any of those dimensions. And boom, now I know how I’m going to solve. When they talk about something but never give you any real numbers for that thing, you’re allowed to pick your own values. Then you can do arithmetic vs. algebra—and we’re all better at working with real numbers than with variables.

My colleagues and I call this Choosing Smart Numbers. The “Smart” part comes from thinking about what kinds of numbers would work nicely in the problem—make the math a lot less annoying to do.

We usually avoid choosing the numbers 0 or 1 when choosing smart numbers because those numbers can do funny things (e.g., multiplying with a 0 in the mix will always return 0, regardless of the other numbers involved).

And if we have to choose for more than one value, we choose different values. Finally, as I mentioned earlier, we’re looking to choose values that will work nicely in the problem. (Most of the time, this means choosing smallish values.)

Finally, before I start solving, I’m going to ask myself two things: What am I solving for and how much work do I really need to do?

I’m trying to figure out how much oil is in the larger (but only half-full!) cylinder. I know that the full capacity of the smaller cylinder costs $2 and that the oil is charged at the same rate for the larger one. So if I can figure out the relative amount of oil in the larger cylinder, I can figure out how much more (or less) it will cost. For example, if it turns out that the larger cylinder contains twice as much oil as the smaller one, then the cost will also be twice as much.

Solve

In the volume formula, the radius has to be squared while the height is only multiplied, so I want to make the radius a lower value. I’m going to choose r = 2 and h = 3.

Use those values to find the relative volumes of the two cylinders. Reminder yet again: The larger cylinder is only half full, so multiply that volume by one-half:

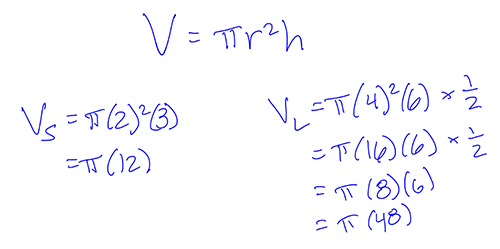
What’s the relative difference between the two? They both contain pi, so ignore that value. The difference is 12 to 48—if you multiply 12 by 4, you get 48.

So the money will also get multiplied by 4: Since the oil in the smaller cylinder costs $2, the oil in the larger one costs (2)(4) = $8. The correct answer is (E).

GMAT Exam 8-Week Study Plan

Reduce your test anxiety by leveraging a solid plan for prep. Follow this link to download the free 8-week study planner.

Learn More

Understand, plan, solve on GMAT Quant

Whenever you solve any GMAT Problem Solving (PS) or Data Sufficiency (DS) problem, follow the Understand, Plan, Solve process. Print out this summary and keep it by you when you’re studying:

Understand

• Glance at the answers (on PS) or the statements (on DS) and the question stem. Anything jump out—an ugly equation, a diagram, an indication that you might be able to estimate, etc?
• Read the question stem. Focus just on understanding what it’s telling you and what it’s asking you.
• Jot down what it’s asking, along with any other useful info (equations, etc.). Don’t solve! Just jot (write or sketch).

Plan

• Reflect on what you know so far. Lost? Guess and move on. But if you do understand everything, then consider what your best plan is. Can you estimate anywhere? How heavily? Can you use a real number and just do arithmetic? Is there a way to draw or logic it out? What are they really asking you? This reflection is how I realized I just needed a relative value on the Oil Cylinders problem.
• Organize your thoughts and your scratch work to get set up for the Solve stage. Maybe you need to redraw or add something to your diagram, as I did for Yolanda and Bob. Maybe you need to group the data or equations a little differently, as I did on the Membership problem.

Solve

• Don’t have a plan you feel pretty good* about? Forget it—guess and move on. (*You don’t have to feel 100% confident. But you want to feel like it’s a decent plan. If you don’t, let it go.)
• Be systematic. You’re almost there. Write your work down. Don’t try to compress steps or work more quickly than is comfortable for you. Keep your scratch paper organized.
• Don’t do more work than you have to. Estimate when you can. Keep an eye on the answers as you work. Eliminate impossible answers as you go. Stop as soon as only one answer letter is left.
• Be willing to bail. Even if you understand and have a decent plan, you still might get stuck. Don’t start trying some other plan at that point. Something’s not working with this one; guess and go spend your time on a better opportunity later in the test.

Finally, remember your overall goal here: You want to go to business school. The point is not to show how much of a mathematics scholar you are. The point is to learn how to think logically about quant topics—with, yes, some amount of actual textbook math tossed in there. 

Actively look for the Logic It Out / Draw It Out / Quick and Dirty approaches. They’ll not only save you time and stress on GMAT Problem Solving and Data Sufficiency, but they’ll also help train your brain for quant discussions in business school and in the boardroom.

Want more strategies to improve your GMAT Problem Solving skills? Sign up for Manhattan Prep’s free GMAT Starter Kit and check out the section on Foundations of Math.

Happy studying!